Hello and welcome!
Since you’re already here, I’m assuming you’re interested in 4D objects, how the human brain works, cognitive neuroscience, and tesseracts. For those who are new to this domain, I’m thrilled to share one of the most fascinating projects I’ve been working on, a journey that takes us beyond the three dimensions we know and into the mysterious world of the fourth dimension.
The broader objective of this study is to investigate how humans and machine learning models perceive, interpret, and mentally rotate objects. If we can understand how the brain truly reacts and adapts to unseen objects, and identify the limitations in the machine learning models’ mechanism, maybe someday we can develop such a model which can work more like the human brain.
But this story is about curiosity. It’s about how our brain can imagine and recognize things we’ve never seen, and how a simple question, “Can the human brain recognize the same 4D object from different angles?”, can open a doorway to understanding how the human brain perceives something new. And here we are talking about the fourth spatial dimension, not time.
Acknowledgement
Before writing about anything, I want to thank someone. This research has been an extraordinary journey, one that took shape under the generous guidance of my research supervisor, Stéphane Deny, Assistant Professor, Aalto University. His insights, encouragement, and vision shaped this project from the very beginning, including the initiative to share our findings through this blog post. I’m deeply grateful for his constant support and thoughtful mentorship.
Thank you, Stéphane, for everything.
Now, take a moment, and get ready to step together into the fourth dimension.
Before diving into 4D objects, let’s begin with simpler concepts to strengthen our understanding, as we’ll need these ideas later in the post to grasp the more complex topics.
What is an object, really?
In everyday life, an object is anything that takes up space, it has width, height, and depth. But in scientific studies, we often use abstract geometric objects instead of everyday things like chairs or bottles. These abstract shapes let us study pure spatial reasoning, free from meaning, experience, or emotional association [1].
What is a mirror image?
A mirror image is a reversed version of an object, as if seen through a mirror. It looks almost identical to the original, but its left and right sides are swapped (when the mirroring is done horizontally, i.e., across the x-axis). For example, when you raise your right hand, your reflection appears to raise its left. In geometry and perception studies, mirror images are important because they test our ability to recognize objects when their orientation is flipped. Even though a mirror image has the same shape and size, our brains sometimes find it challenging to tell whether it’s the same object or a mirrored one [2, 3].
Here is an example of a mirror image:
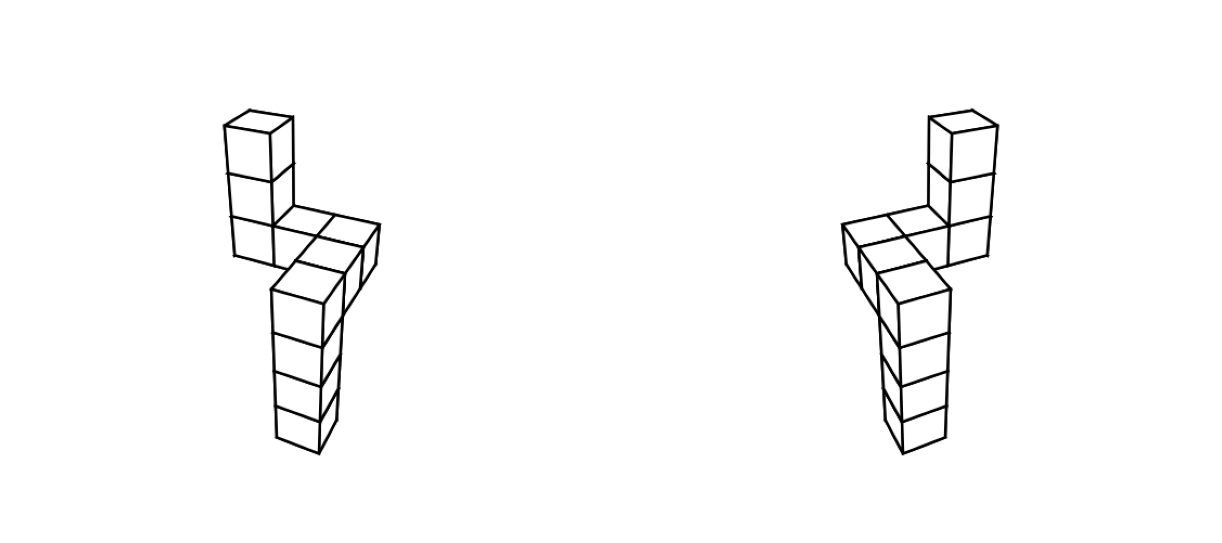
Figure: Mirror object – if left is the real object, right one is the mirror and vice versa, (courtesy: Aleksandr Sasha Krylov)
The Shepard-Metzler shape
In 1971, Roger Shepard and Jacqueline Metzler introduced a classic experimental setup [3], a pair of 3D objects built from small connected cubes in random configurations (10 or 12 cubes), known today as Shepard-Metzler shapes. Participants in their experiment were shown two such shapes and asked: “Are these two the same object, or are they mirror images?”
The result was remarkable: the more the object was rotated, the longer it took people to recognize it. Reaction time increased almost linearly with the angle of rotation, as if people were physically rotating the object in their minds [3]. This discovery revealed something deep about the human imagination, it doesn’t just see, it simulates. The mind follows geometry, and this is where the theory of mental rotation begins.
Here are some images of 3D Shepard-Metzler shapes made with 10 cubes:
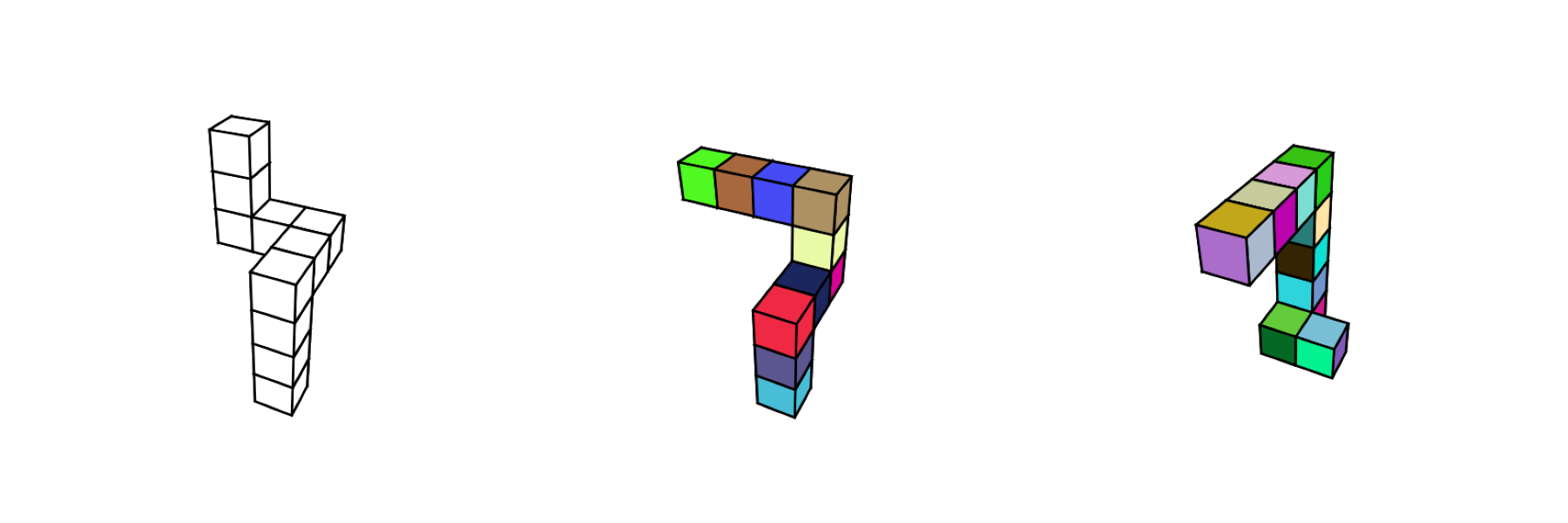
Figure: 3D Shepard-Metzler shapes, (courtesy: Aleksandr Sasha Krylov)
Mental rotation
Mental rotation is the process of imagining an object turning in space to determine whether two shapes represent the same object viewed from different angles [3, 4]. For instance, when we see two 3D objects in different orientations or angles, we can mentally “spin” one to align it with the other. This act of mental manipulation involves performing rotational transformations in the mind, just like physically turning an object around its axes, to compare their spatial structures and recognize whether they are identical or mirrored.
The question that started it all
For decades, researchers have explored mental rotation in two and three dimensions, investigating how it varies with expertise, training, or age. In today’s era of technology and artificial intelligence, scientists are even teaching machines to perform similar tasks, asking models to recognize whether two Shepard-Metzler shapes are the same or mirrored. Humans can effortlessly identify 3D objects, even when viewed from different angles, but machine learning models struggle with such recognition on unseen data.
This difference raises a fascinating question: is the brain’s remarkable performance due to its information processing mechanisms, or is it simply because we have spent a lifetime immersed in a 3D world? In other words, does true “novel” test data even exist for humans in three dimensions?
This brings us to the new research question: how would the brain respond if the testing data were genuinely novel? For instance, not in 3D space, maybe something in 4D, such as a tesseract? Would the human brain perform as well as it does with 3D objects, or would its performance differ?
To explore this, we decided to step beyond the limits of ordinary perception by introducing four-dimensional objects that extend an additional spatial axis, w, alongside x, y, and z (x, y, z, w) to see how the human brain reacts to something it has never seen before.
And that’s where our journey truly begins: into the mysterious world of the fourth dimension.
What Is a 4D object?
A four-dimensional (4D) object extends the concept of space by adding a new axis, one that is perpendicular to all three familiar ones.
In 2D, we have (x, y)
In 3D, we add another dimension (z), making it (x, y, z)
Similarly, in 4D, we introduce a new direction (w), resulting in (x, y, z, w)
We can’t see or move along this fourth axis directly, but we can represent it mathematically. And just as a 3D object creates a 2D shadow, a 4D object can make a 3D projection that we can visualize [5]. The most famous example of this phenomena is the Tesseract, the 4D analogue of a cube [6]. A tesseract has eight cubic “faces”, connected through the fourth dimension. When it rotates, it appears to fold into and out of itself, a mesmerizing dance that hints at the geometry beyond our regular world.
From theory to visualization
Our goal was to make the invisible visible, to create a way for people to see and interact with 4D objects. To do that, we built a custom OpenGL-based renderer that projects 4D tesseracts into 3D, and then onto a 2D display. By rotating the tesseract through different 4D planes, such as x-w or z-w, we can simulate what a 4D object might look like if we could perceive it directly.
Here is the look of our transparent Tesseract:
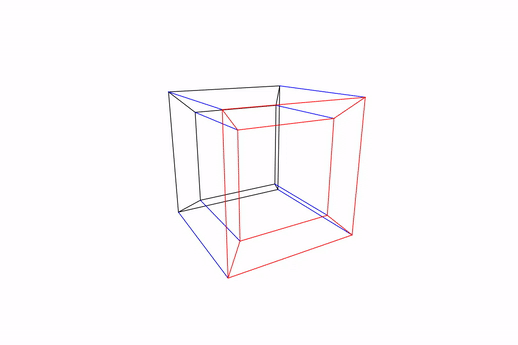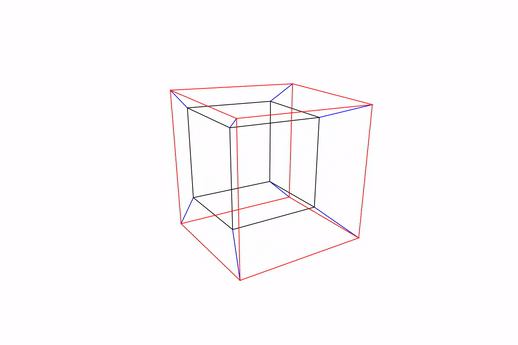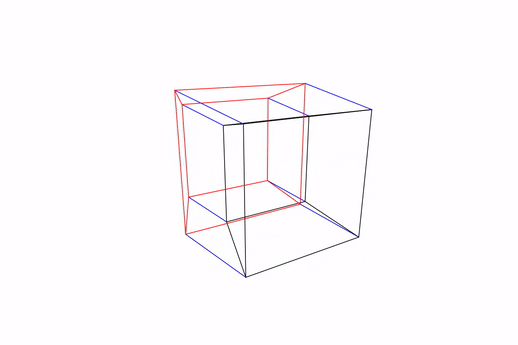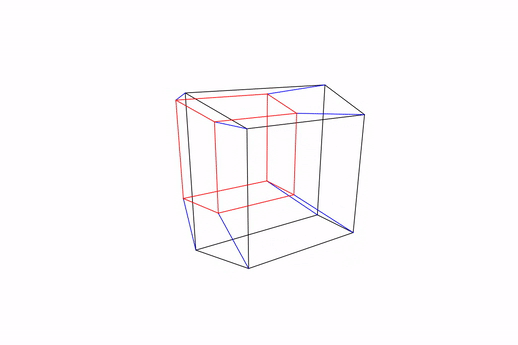
Figure: Tesseract rotating in its z-w axis
Here is what it looks like when rotating along another, non-special axis:
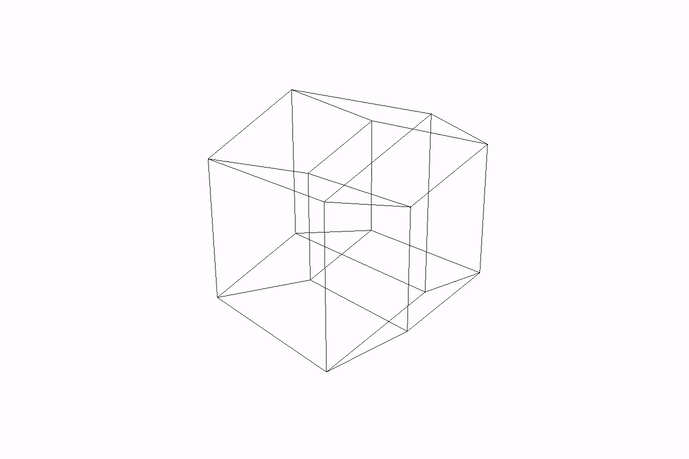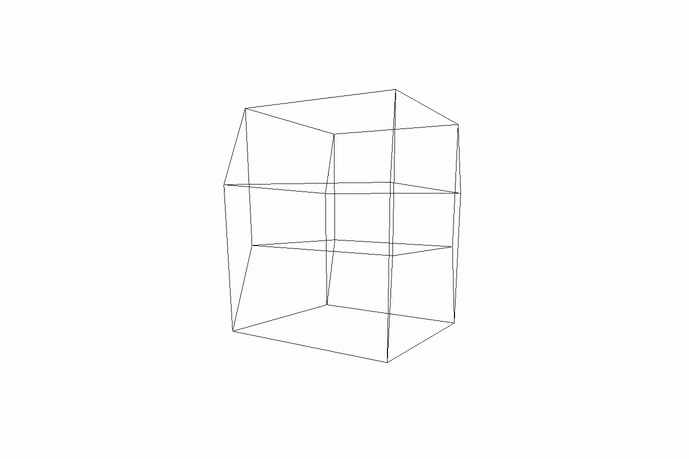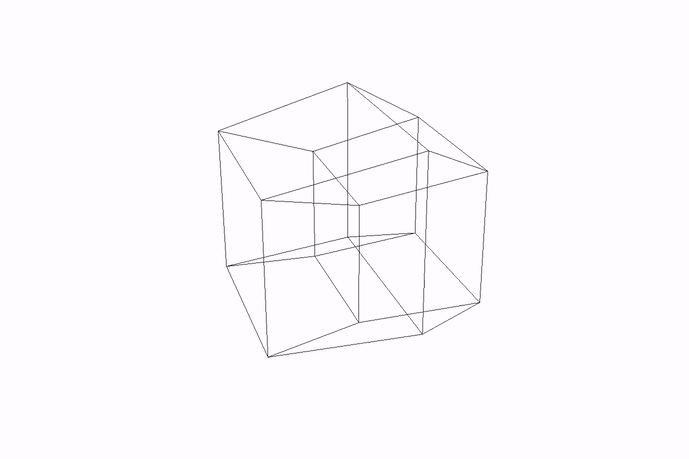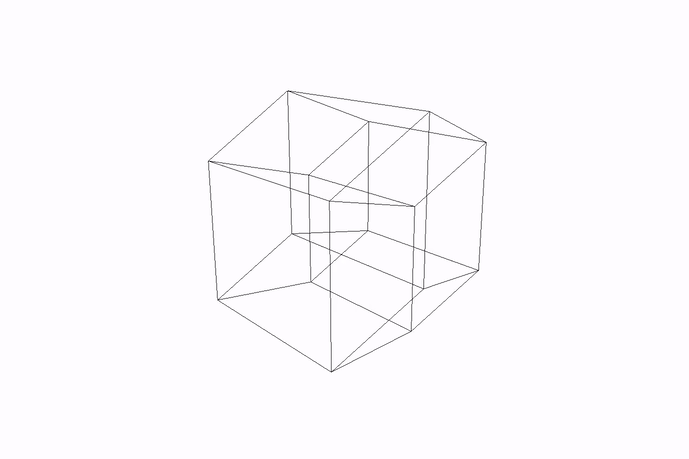
Figure: Tesseract rotating in non-special axis
And later, we made it opaque for our experiment setup. Here’s how it looks:
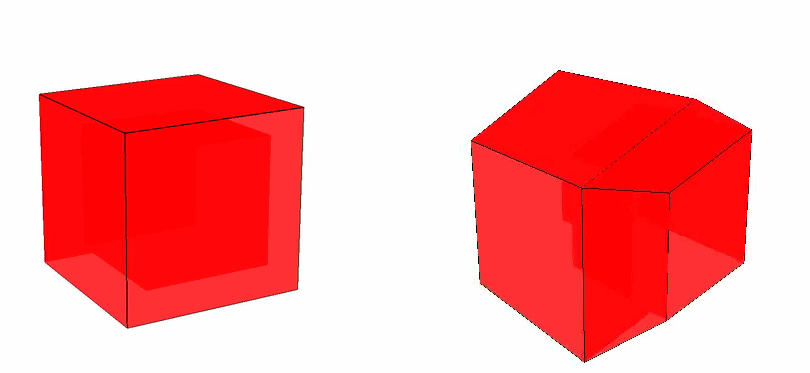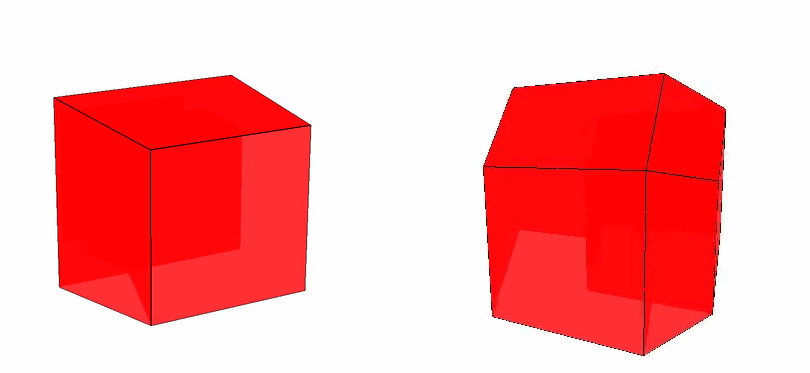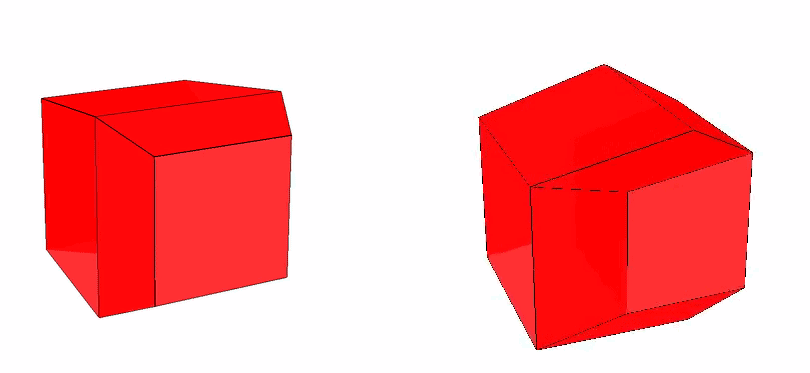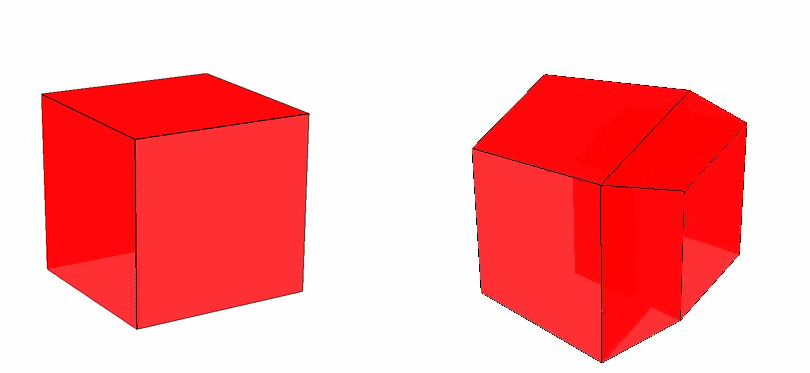
Figure: Tesseract with 90 percent opacity
We then adapted the idea of the classic Shepard-Metzler shapes into the fourth dimension. Instead of connecting cubes in 3D, we connected 4D cubes, or hypercubes, to form complex structures that we now call 4D Shepard-Metzler shapes. How we generated these 4D Shepard-Metzler shapes and visualized them on 2D screens through coding and mathematics is a different story, I’ll share that in detail in one of the next episodes.
The human experiment
With these 4D shapes ready, we made a setup for an experiment where participants view two 4D Shepard-Metzler shapes and must decide whether they are the same or mirror images. Each shape can also be mirrored along a 4D axis. The trials were randomized, and every response time was recorded down to the millisecond. This setup lets us measure how quickly and accurately people can mentally rotate objects that their visual system has never encountered before.
Typically, when a mental rotation experiment takes place in 3D, it looks something like this:
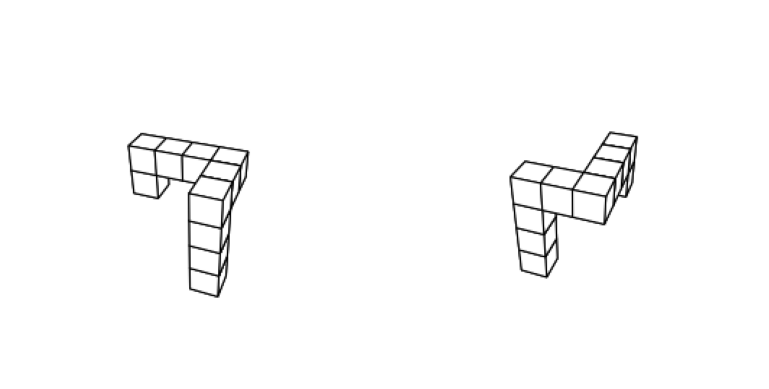
Figure: a pair of 3D Shepard-Metzler shapes made with 10 cube each (courtesy: Aleksandr Sasha Krylov)
But in our 4D setup, it looks like this:

Figure: a pair of 4D Shepard-Metzler shapes made with 12 tesseracts each
Strange, isn’t it? Since the object exists in four dimensions, it naturally appears very different from what the human brain is used to perceiving. And that’s precisely the purpose of our experiment, to explore how the brain reacts when faced with completely novel, unfamiliar objects that go beyond its everyday experience.
Even more surprisingly, these two images are from the same 4D Shepard-Metzler shape viewed from different angles. If you don’t believe it, watch the rotating video of the same shape and see for yourself.
Video: A 4D Shepard-Metzler shape made with 12 tesseracts rotating across y-axis
What we’ve learned so far
Early findings show that humans can interpret 4D rotations, though more slowly and less confidently than in 3D. It seems that the brain is trying to use its 3D reasoning skills in a 4D world, and while those skills partly work, they don’t always fit perfectly.
However, this experiment is still in its very early stage. We need to test it with a larger number of participants before going to any solid conclusions. With more data, we will be able to compare the reaction times to those in the classic 3D Shepard-Metzler experiment and examine whether the relationship between reaction time and the angle of rotation remains linear in four dimensions.
Future Work
We have not yet conducted this experiment with machine learning models. We have two plans in the pipeline for that. The first is to train a model on 3D Shepard-Metzler shapes and then test it on 4D shapes to see how well it performs with that level of prior knowledge. The second is to train the model directly on 4D Shepard-Metzler shapes and test it again to compare the results and understand the difference in performance.
Takeaways
Studying how humans imagine higher-dimensional objects doesn’t only teach us about perception, it can also inspire new ideas in artificial intelligence. If our brains can understand this unseen dimension, machine learning models could be designed to do the same, to generalize across dimensions, rather than staying confined to their training data. This bridge between cognitive neuroscience and AI opens exciting questions about how intelligence (human or artificial) perceives structure in the world.
Upnext
Spaceland – Ep. 02 – From Equations to Perception: Generating and Visualizing 4D Shepard-Metzler Shapes
References
- Biederman, I. (1987). Recognition-by-components: a theory of human image understanding. Psychological review, 94(2), 115.
- Corballis, M. C., & Beale, I. L. (2020). The psychology of left and right. Routledge.
- Shepard, R. N., & Metzler, J. (1971). Mental rotation of three-dimensional objects. Science, 171(3972), 701-703.
- Mental Rotation (Stanford Encyclopedia of Philosophy/Winter 2015 Edition). (2015). Stanford.edu. https://plato.stanford.edu/archives/win2015/entries/mental-imagery/mental-rotation.html
- Rucker, R. (2014). The fourth dimension: Toward a geometry of higher reality. Courier Corporation.
- Wikipedia Contributors. (2019, September 15). Tesseract. Wikipedia; Wikimedia Foundation. https://en.wikipedia.org/wiki/Tesseract